比例、１次関数とは？

比例、1次関数はそれぞれ「2つの数の関係をあらわす式」です。

比例とは

比例は、2つの数の関係のうち、最も単純なものです。生活にもよく活用されています。

例えば、とあるスーパーマーケットで、お肉が100g当たり200円で売られています。

お肉を200g買えばお会計は400円、300g買えばお会計は600円となります。

お肉を買う量が2倍になればお会計も2倍に、3倍の量を買えばお会計も3倍になる、というのが比例の関係です。

この場合、お肉の値段を1g当たりに直すと2円になるので、お会計の値段をy（円）、購入したお肉の量をx（g）とすれば、y=2xとあらわすことができます。

このようにy=ax（a≠0）であらわせるとき、「yはxに比例する」といいます。

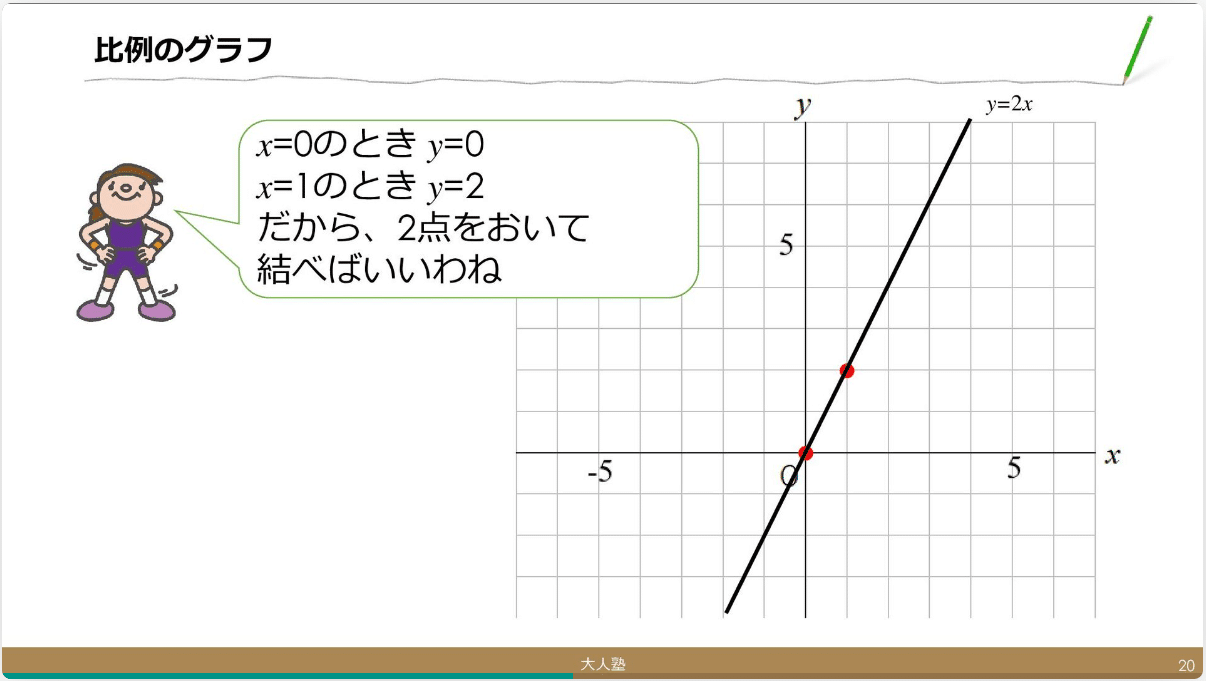
これをグラフにすると次のようになります。

比例の関係を理解することで、1次関数や2次関数の理解もより深まります。

1次関数とは

1次関数は、比例の考え方を一歩進めたものです。

1次関数の考え方は、数学だけではなく、実生活、ビジネスにも役立ちます。また、高校で習う微分にも応用できます。

1次関数は、y=ax+b(a≠0)とあらわせます。

比例の式y=ax（a≠0）と比べると、　「+b」　の部分が違うことがわかりますね。

グラフにすると以下のようになります。

そもそも関数とは

関数とは、一方の数が決まるともう一方の数が決まる式を指します。

xの値は、自由に変えることができます。それに伴い、yの値が確定します。このx,yを変数といいます。また、xの値を決めると、yの値が1つ決まるとき、y は x の関数といいます。

Excelの関数も同じ意味です。
何かの値を入れることで、出力する値が変わります。

傾き、切片などの言葉の解説は、下記のスライドをご覧ください。

大人塾ではこのようなスライドを見ながら学習を進めていきます。

1次関数

鈴木さんが正午から毎分50mの速さで移動したとします。

移動距離をy、時間をxとするとy=50xという関係が成り立ちます。この式は比例です。

鈴木さんが、正午の時点で家から300m離れた場所におり、その後、毎分50mで移動したとすると、y=50x+300 という式にあらわせます。

先ほどの比例の例と比べてみると、xのあとに+300がついていますね。

このようにy=ax+b（a≠0）の形で表せるとき、「yはxの一次関数」といいます。また、比例は一次関数のb=0のときであることがわかります。

aは変化の割合（後で出てきます）と、bは最初の位置である300と対応していることがわかります。

このとき、y=ax+bのbにあたる数を切片といいます。上の例では300です。

増加量と変化の割合

1次関数では、増加量や変化の割合といった難しそうな言葉がでてきます。言葉の意味をしっかりと理解しましょう。

増加量

増加量というのは「（後の量）ー（前の量）」のことです。

例えば、現在の所持金が3万円だとします。

そこで、口座から5万円引き出すと所持金の増加量はどうなるでしょうか？

所持金は、合計で8万円になるので、所持金の増加量は8万円-3万円=5万円です。

所持金が3万円のとき、1万円支払うと、残りのお金は2万円です。

このときの増加量は2万円ー3万円＝-1万円です。

増加量といいながらも値がマイナスになることがあるのがややこしいところですよね。

変化の割合

変化の割合とは「（あるものの増加量）÷（単位になるものの増加量）」のことです。

鈴木さんが正午から12時10分まで散歩をして、500m移動したとします。

移動距離の増加量は500mー0m=500m、時間の増加量は12時10分ー12時0分＝10分です。

このとき、変化の割合は（移動距離の増加量）÷（時間の増加量）＝500m÷10分＝50m/分となります。

つまり今回の場合は、変化の割合が速さと一致しています。鈴木さんは1分当たりどれくらい移動するのか？ということですね。

1次関数やそのグラフを理解することができれば、連立方程式の解の意味に気づけたり、損益分岐点を計算をしたりすることもできます。

比例と一次関数をしっかり学ぶなら

比例と一次関数を基礎から学びたい方は、大人塾の「比例と一次関数」コースがおすすめです。

学習内容

比例と反比例、一次関数の式の違いや1次関数の解き方、グラフの書き方、連立方程式と1次関数、1次関数の変域、そして（1部では大人気の）動く点Pなど、1次関数について、しっかりじっくり学ぶことができます。

このような方にもおすすめです

2次関数の前提学習としても学ぶことをおすすめいたします。

カテゴリー: 解説

タグ: 1次関数一次関数反比例比例

比例とは